Single phase Inverter synchronization to mains using time continuous phase angle approximation with analog components

For impatient visitors, the LTspice model download is at the bottom of this post.

In our previous post we discussed the method that uses ZCD + flip-flops to extract the phase angle (angle of synchronism) using pulses whose duty cycle is proportional to the phase angle, and with a pulsing frequency of 2*f_ac, f_ac being the working frequency of the mains (grid) and inverter. Although this method is robust in the case of voltage variations, feeding pulses to our control loop required a more agressive low pass filtering strategy, and has a low gain at minimal phases angles, Overall it makes the control loop tuning harder.

So we will propose now a time continuous analog estimation of phase angle. It closely resembles to the single multiplier phase detector in the shape of the output, but does not involve a multiplier. This method is projected to be significantly more sensitive to voltage swells/sags and transients or voltage imbalances between the mains and the inverter, as it is the case for most phase detectors used in PLL. So it will involve signal normalization as well. We will try to characterize the performance of this method compared to the classic mutiplier based phase detector. Same as in the previous post, here we are discussing of synchronized inverters, not grid tied ones. As such, these inverters, perform voltage control independently of the grid conditions, that is one of the main benefits of the double conversion (online) topology, that always supplies power coming from the inverter stage at a stable regulated voltage while the grid voltage may fluctuate. On the other hand, line interactive or offline UPS perform AVR only using an autotransformer with taps to buck or boost a voltage by fixed increments. Since we have a potentially fluctuating grid voltage due to external conditions and a UPS voltage regulated at a nominal value, (not taking into account voltage fluctuations due to regulation inertia), it is important to characterize the sensitivity to voltage imbalances of the following method to assess its viability for the purpose of inverter phase synchronization.

Principle of operation

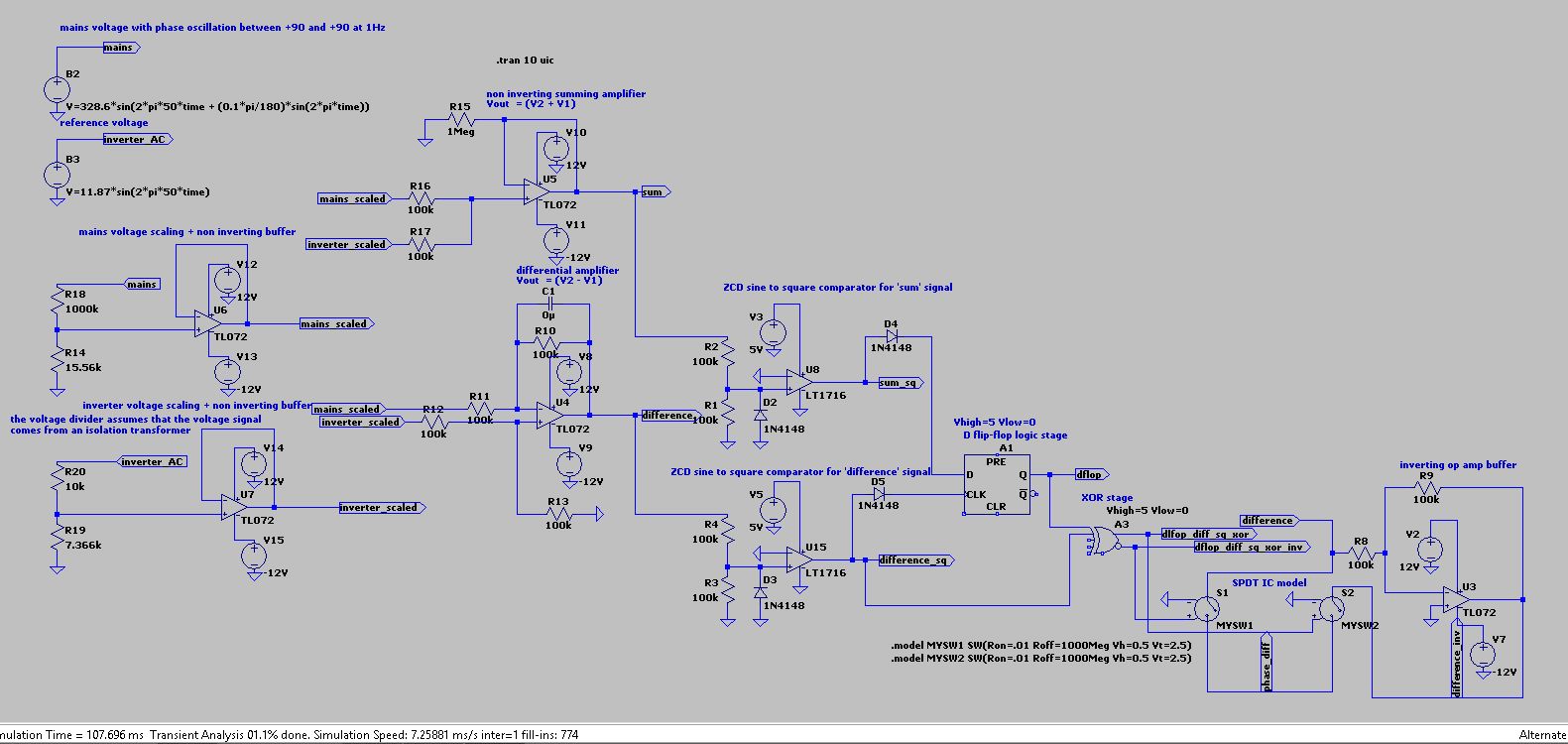
Instead of supplying the control loop a pulse whose duty cycle is proportional to the phase angle, with a postive pulse for positive phase angles and a negative pulse for negative phase angles. We supply the control loop the differential signal of V_mains(t) and V_inverter(t). That is V_mains(t) – V_inverter(t), after scaling the source signal to a level compatible with op-amps. Although it works to extract the absolute phase angle, assuming that the two voltages are of the same amplitude, preserving the lagging/leading information, that is the sign of the phase angle, requires careful processing of that signal.

Assuming a constant phase angle different than 0° and that the amplitudes of V_mains(t) and V_inverter(t) are the same,

We can see that the V_mains(t) – V_inverter(t) changes sign when V_mains(t) = V_inverter(t), although the lagging/leading status is still the same. That is why we need to switch the V_mains(t) – V_inverter(t) signal to -(V_mains(t) – V_inverter(t)) when V_mains(t) = V_inverter(t), to preserve lagging/leading information.

To encode the instant where V_mains(t) = V_inverter (t) using a basic sine to square circuit, we will feed the scaled down sum signal, (labeled ‘sum‘ in the schematic) V_mains(t) + V_inverter(t) to a comparator to get a square wave signal. The rising edge will happen at zero crossing going upwards of V_mains(t) + V_inverter(t), The falling edge at zero crossing going downwards. The points where V_mains(t) = V_inverter(t) will sit firmly at the middle of each HIGH or LOW levels time intervals. The resulting square wave signal is labeled ‘sum_sq’ in the LTspice model.

To establish a processing logic, We will also need to convert the difference signal, labeled ‘difference’ in the schematic into its corresponding square wave signal. This resulting signal is labeled ‘difference_sq‘ in the LTspice model. Note that the difference_sq signal switches polarity, that is, goes from RISE to FALL or vice versa at the points where V_mains(t) = V_inverter(t). More precisely, it is rising at V_mains(t) = V_inverter(t) when both V_mains(t) and V_inverter(t) are positive, and falling at V_mains(t) = V_inverter(t) when both V_mains(t) and V_inverter(t) are negative.

We used the LT1716 comparators for the ZCD sine to square conversion. It also conditions the square signals to 5V logic levels. It is tolerant to an input going down to -5V in relation to negative rail, here GND, while still outputing a valid 0V output in this case. This information is available in the datasheet.

Next we will establish a truth table for the above two signals.

TRUTH TABLE	difference_sq RISE	difference_sq FALL
sum_sq HIGH	1	0
sum_sq LOW	0	1

Note that we compare an edge signal to a level signal, for this edge triggered logic, a D type flip-flop comes handy. You may also ask why we need this convoluted logic, well it is necessary in order to preserve the leading/lagging information. In order to do that, we will need an additional logic stage between the above resulting signal, labeled ‘dflop‘ in the model, and the difference_sq signal. This time both signals are levels, so to establish the following truth table we will simply use a XOR gate.

TRUTH TABLE	difference_sq HIGH	difference_sq LOW
dflop HIGH	1	0
dflop LOW	0	1

The resulting signal will condition the state of the SPDT switch IC, the ADG333A IC is suitable for this application. The silicon SPDT switch will switch the output between $$ difference $$ and $$ \overline{difference} $$ input signals.

And that’s how we get an approximation of the phase angle, preserving the leading/lagging information. Note that the logic signal coming into the silicon SPDT switch not only has the result of switching polarity of the difference signal when the phase angle goes from leading to lagging and vice versa, but also performs rectification of the difference signal.

To better illustrate the action of the whole signal conditioning logic, we provide the following screen capture :

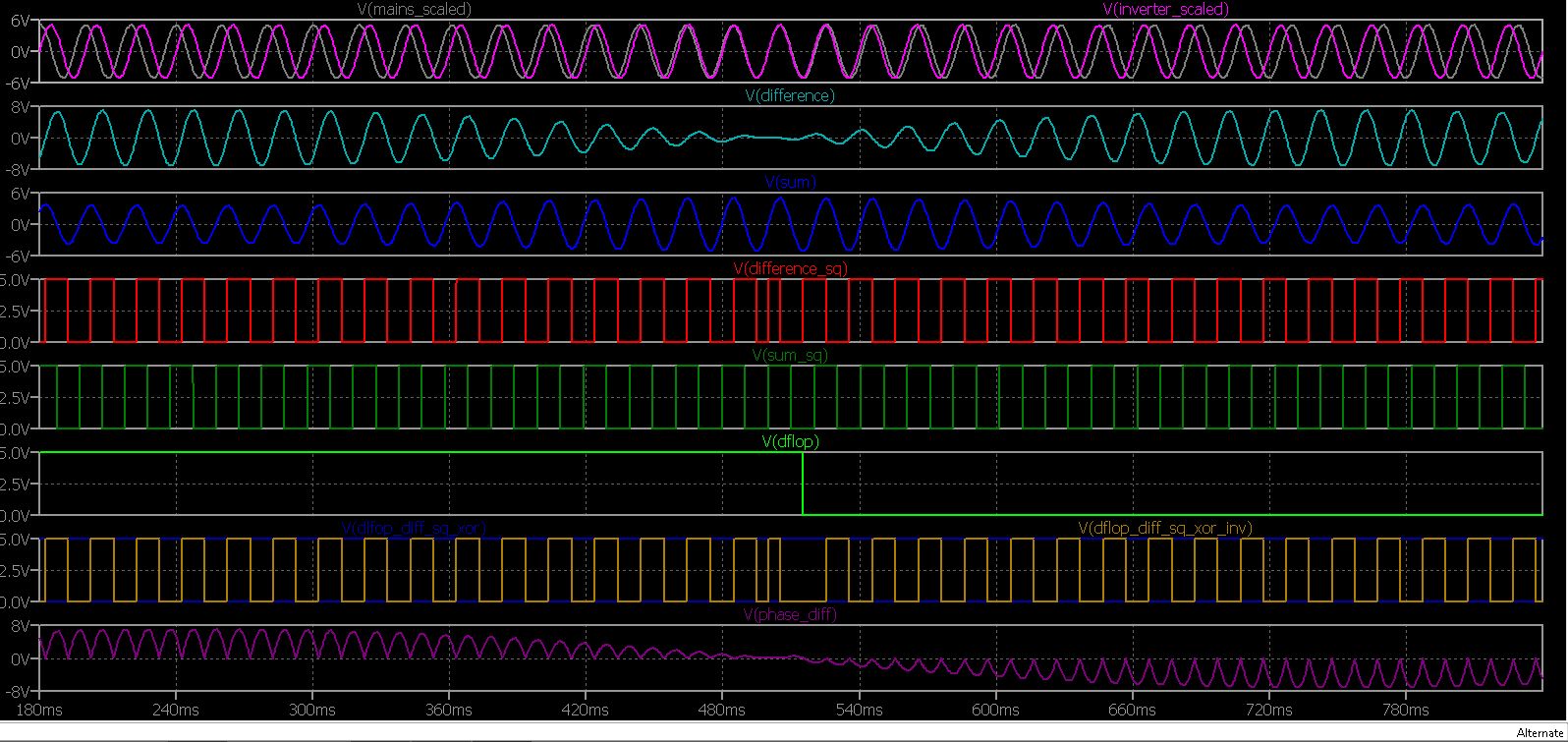
Now that we have our proper phase angle approximation signal, it is time to feed it to the control loop.

Remember from our previous post that, assuming same frequency and voltage for both signals, and a constant phase shift or a phase variation frequency that is negligible compared to f_ac :

$$ (1)\hspace{1cm} \left | \Delta \varphi \right | = 2arcsin(peak( \frac{\left |V_{mains}(t) – V_{inverter}(t)\right |}{2V_{max}} )) $$

with peak() defined as the function that returns the peak value as a step function over the time range of interest defined below.

Note that for : $$ (2)\hspace{1cm} \left | \Delta \varphi \right | \ll \pi $$

$$ (3)\hspace{1cm} \left | \Delta \varphi \right | \approx peak( \frac{\left |V_{mains}(t) – V_{inverter}(t)\right |}{V_{max}} ) $$

Being sinusoidal in nature, it follows that for a time interval $$ (4)\hspace{1cm} \left [ t_{1} , t_{1} + \frac{1}{2f_{ac}} \right ] $$ or multiple thereof,

(3) is a linear relationship because $$ (5)\hspace{1cm} peak(k\times a(t)) = k\times peak(a(t)) $$ provided that (2) is true. Note that for the ZCD discrete phase angle method of our previous post, there is a linear relationship over the whole [ -pi , pi ] domain.

The main difference then lies into the LP stage filtering response of our control loop between a variable duty cycle bipolar square wave signal with 2*f_ac frequency and a bipolar sinusoidal signal with rectified sine harmonics at 2*f_ac frequency.

Phase angle control loop

We reused at first the phase control loop from our earlier post design :

https://www.skynext.tech/index.php/2023/01/16/single-phase-inverter-synchronization-to-mains-phase-using-the-zero-crossing-method-and-proportional-derivative-control-with-analog-components/

Since this post, it has been updated with an additional integral term to get a PID control loop.

This loop already gave relatively good results (phase angle < 0.75° for most disturbances in our simulation bench). We used it too gather data in the new phase continuous model as a reference for improvement.

Then, we optimized the loop design to get a better phase response. For this, we got rid of the butterworth filters after the integral and derivative stages, as well as a tuning of the integral cutoff frequency and the derivative peak response frequency. We will post both results here as well as the Bode plot of the new control loop.

Voltage imbalance sensitivity

Voltage amplitude imbalance between mains_scaled and inverter_scaled has effects on the diff_out signal that are mostly characterized by a reduced sensitivity to small phase angles. The signal shows a larger DC bias, which swamps the response to angle variations.

The leading/lagging transition response seems less affected, the system being able to detect the transition in small phase angle oscillations, even in the presence of a moderate voltage imbalance.

Let’s discuss the possible mitigation strategies of the voltage imbalance sensitivity.

For the purpose of phase synchronization outlined above, the inputs of the control system are :

• Inverter voltage sensing coming from an isolation transformer on the output of the inverter.
• Mains/grid voltage sensing coming from another isolation transformer

Both of these inputs could also be used for voltage (amplitude) sensing. Inverter voltage sensing is already used for inverter voltage (feedback) regulation. If we wish to compensate the voltage imbalance for phase synchronization, we may need to sense both.

Voltage amplitude sensing methods usually implement peak detection using smoothing capacitors and a full bridge rectifier.

Inverter voltage is dictated by the inner voltage/current control loop and possibly an outer control loop. It is subject to a certain amount of inertia. Moreover, set/regulated voltage may well be different than the nominal 240V AC.

Mains/grid voltage is dictated by the grid. We also have to take into account the serial impendance of the transmission line and that of the 10kV/240V utility transformer. These will produce a voltage drop dependent on the load, and account for a large portion of voltage variation during the day.

If, for whatever reason we wish to implement the proposed method above we would need to get rid of the voltage amplitude difference.

• Either we establish the mains voltage as a reference, and make the inverter follow it, by controlling the amplitude of the independently generated sine wave reference of the SPWM modulator. In that case, it defeats one of the main purpose of an inverter, specially for online (double-conversion) UPS, which is voltage stability independently of the grid.
• We could also use the mains voltage as a reference to the full extent, after scaling it down, by using the mains voltage waveform as the sine wave reference used in the SPWM generation, in that case, the inverter also follows frequency and phase of the grid as a bonus, which render the whole synchronization issue of the present article moot. The downside is that the inverter output is now subject to all disturbances of the grid, including transients, noise, etc… if adequate filtering is not provided. The inverter now works as a class-D amplifier.
• Third option, we establish inverter voltage as a reference, and make the mains (scaled down voltage input) follow the inverter voltage in terms of amplitude. Since we have no control on the voltage from the grid, the only method that seem plausible would be to perform AGC (automatic gain control) on the sensed mains voltage to make it follow the sensed inverter voltage.

The later is not without problems though. We predict that there may be quite a high amount of crossover interaction between the phase/frequency control loop and the voltage/current control loop, making tuning of both difficult. Let’s try nevertheless.

Implementing AGC on mains voltage sensing

Since an inverter voltage control loop usually implements voltage sensing for its output using a peak detector (with attack/release control), And that doing the same for the mains voltage is also usually a requirement, for instance, to detect voltage sags/swell that go beyond the AVR capability, or simply for mains blackout detection, it seems that it would not cost much to at least try to implement an AGC for the goal of phase angle synchronization using the peak detectors outputs as differential inputs to generate a voltage control signal based on the voltage error that will be subsequently applied to a VCA. The VCA will perform AGC on the scaled mains voltage signal to keep it at the same amplitude that of the scaled inverter voltage. Then phase angle measurement can be performed without worry about the effect of amplitude imbalance.

The VCA would not need to have fancy requirements. It does not need high bandwidth, since it will work on a 50 Hz signal. It does not need high dynamic range, since it will operate on a mains voltage plus/minus 20% (worst case scenario) deviation from the nominal 240V AC. (Mains voltage is required in Europe to stay in the plus/minus 10% range from the nominal 240V AC.)

However, It would preferably use linear voltage control of the gain. That is to ease the loop design and tuning.

Voltage transient filtering (or what remains of it after the TVS upstream) could be achieved by tuning the attack potentiometer of the peak detector stage. However a compromise should be found between a good transient response and a good voltage following response so as not to introduce too much delay. This is not an easy task.

Given the requirements, a TI VCA824 IC seems a good choice. Other options although not tested would be to use an OTA like the LM13700, Finally we could also use an audio VCA like the THAT 2180x series, but it also OTA-like since it sources/sink current at the output, so either a resistor or better a current to voltage op-amp block is needed at the output. However the THAT 2180x is an exponential (dB/V) voltage controlled device, Whereas the VCA824 IC is linear (V/V). An advantage of the THAT 2180x is that it features a 0dB gain at 0V center point. It is not the case for the VCA824, Where the unity gain is closest to 0V gain control for a 2V/V max gain setup (dictated by the Rf/Rg feedback resistor setup). Even with a 2V/V gain setup the unity gain point is not exactly at 0V (at least in our setup). But this is not that much of a problem since there is a control loop for amplitude that takes care of it. Other issue encountered with the VCA824 IC is that we had to correct input and output offset voltages using voltage dividers at the signal input and output as shown in the datasheet. Using AC coupling for that purpose is a big no no since it would introduce delay. Finally, there is the cost issue. VCA824 is expensive and its features underutilized since it is tailored for HF/VHF use. But it works well for VLF like 50 Hz too. Finally, there is the issue of dynamic range. VCA824 can’t take much more than ± 1.6V at input, and goes sensibly lower than ± Vs for the output. Here Vs is ±5V (rail to rail) and this is the max for safe operation. To get some operational margin for voltage sags and swells, we setup max gain at 3V/V, and the whole setup works so as to obtain a normalized 1V amplitude mains signal, whatever the voltage sag/swell condition is. We expect the setup to be more sensitive to noise because of the reduced signal amplitude that is fed to the continuous phase angle measurement logic.

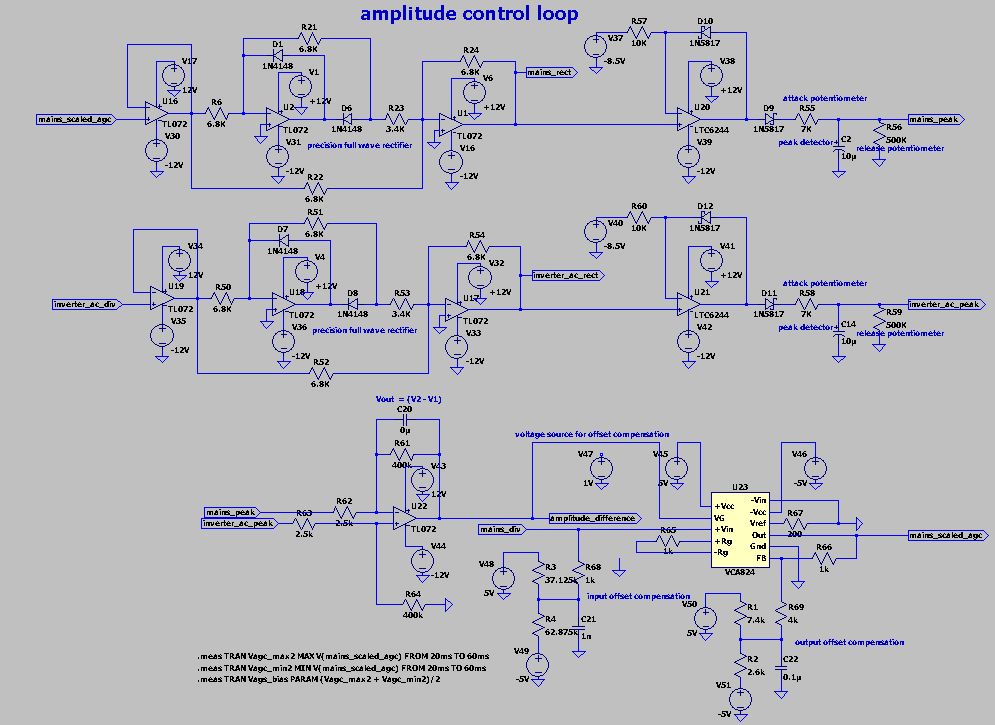
Amplitude disturbance

For now, we only considered single tone FM disturbance of mains grid voltage. We still have to tackle amplitude disturbance like fast voltage transients with a clamped profile (from the TVS action), temporary overvoltages/undervoltages (from load rejection / load connection events in a generator setup), and slow voltage daily/hourly variations due to load profile change across several utility subscribers sharing a 11kV/230kV transformer.

First we will test the performance with a static voltage deviation from nominal 230V and see how the AGC performs, and how the whole loop behaves.

<to be continued>

Harmonics Disturbance

This is the hard part. It is expected that with a good voltage following characteristic, the whole loop would also somewhat track harmonics from the grid. Our goal would be to track the phase and frequency of the fundamental, not the harmonics ladden signal. We could think that filtering the mains signal would be a good idea, However we would need a really flat phase response (like those of Bessel filters), and even with that, we would need to compensate the delay with something like an all pass filter tuned to bring the 50Hz signal to a 360 phase or multiple thereof. That would introduce phase problems for frequencies other than 50Hz. Moreover, Bessel response is inadequate to filter the third harmonic sufficiently since it is so close to the fundamental. We could use a Butterworth LP filter but phase response issues would be even worse with each increasing order. We could think of a really good rejection of harmonics with a resonant filter, but that would be the absolute worse of the worse in terms of phase issues. Harmonics rejection is at the current state of analog filter technology an intractable issue in our opinion and would be better tackled in the Z-domain. Comment if you disagree.

Nevertheless, we added a harmonics disturbance setup in our model with 3rd,5th,7th,9th and 11th harmonics setup with amplitude (in % of fundamental amplitude) and phase (for each harmonic) to characterize the performance. At this point, the equation (3) is unsuitable, unless we compare the output sine reference to the fundamental of the harmonics disturbed signal.

Simulation Model

The simulation model includes the ASC Ltspice file with all packages dependencies (asy,sub,lib) in the same folder. There should be no need to tweak inside the file for absolute paths as they have been removed. No non-standard diodes, fet, bjt are used so there should be no need to add lines in the respective files (such as standard.dio or standard.bjt)

This model only models the PLL, not the full inverter. It’s goal is to generate a synchronized sine reference from mains voltage, and be tolerant to voltage sags/swells, frequency variation as well as harmonics. Harmonics should be rejected in the sine reference as much as possible.

Recently I added a block to simulate ADC operation with with sample time quantization and amplitude quantization to more accurately simulate an AD7366 ADC.

It includes a test bench block to simulate :

• Amplitude disturbance
• Frequency disturbance
• Harmonics disturbance
• Initial phase angle

It also includes the PLT files for plotting.

More information available in ____README____.txt inside the zip archive.

Have a nice day !